User:Tomruen/Noncrystallographic root systems
Appearance

There are just a few irreducible noncrystallographic root systems: H4, H3, H2, and I2(p) for p=5,7,8....
Folding A4, D6, and E8
[edit]These can be constructed from simply laced root systems. H4 is a folding of E8, H3 is a folding of D6, and H2 is a folding of A4. A final H1 can be seen as a folding of A1A1. The ratio in length of the long to short roots is the Golden ratio, φ.
- A1A1 has 4 roots, from a square, {}×{},
 , being the vertex figure of the apeirogon product:
, being the vertex figure of the apeirogon product: 





 .
.
- H1, as a folding of A1A1:




 , has 2 sets of 2 root, each seen as the vertices of a digon:
, has 2 sets of 2 root, each seen as the vertices of a digon:  .
.
- H1, as a folding of A1A1:
- A4 has 20 roots, from runcinated 5-cell polytope, t0,3{3,3,3},






 , being the vertex figure of the 5-cell honeycomb and A4 lattice:
, being the vertex figure of the 5-cell honeycomb and A4 lattice: 



 .
.
- H2, as a folding of A4:


 , has 2 sets of 10 roots, each seen as the vertices of a decagon:
, has 2 sets of 10 roots, each seen as the vertices of a decagon: 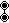
 .
.
- H2, as a folding of A4:
- D6 has 60 roots, from the rectified 6-orthoplex polytope, t1{3,3,3,31,1},








 , being the vertex figure of the 222 honeycomb and D6 lattice:
, being the vertex figure of the 222 honeycomb and D6 lattice: 







 .
.
- H3, as a folding of D6:




 , has 2 sets of 30 roots, each seen as the vertices of a icosidodecahedron:
, has 2 sets of 30 roots, each seen as the vertices of a icosidodecahedron: 



 .
.
- H3, as a folding of D6:
- E8 has 240 roots, from the 421 polytope, {3,3,3,3,32,1},












 , being the vertex figure of the 521 honeycomb and E8 lattice:
, being the vertex figure of the 521 honeycomb and E8 lattice: 













 .
.
- H4, as a folding of E8:






 , has 2 sets of 120 roots, each seen in the vertices of the 600-cell:
, has 2 sets of 120 roots, each seen in the vertices of the 600-cell: 





 .
.
- H4, as a folding of E8:
| A1A1 → H1+φH1 | A4 → H2+φH2 | D6 → H3+φH3 | E8 → H4+φH4 |
|---|---|---|---|
4 roots 2×2 roots |
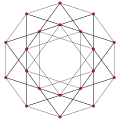 20 roots 10×2 roots |
 60 roots 30×2 roots |
 240 roots 120×2 roots |
Rank 2
[edit]| Simply-laced group folding |
D2 A1+A1 |
A2 | A3 to B2 D2+√2 D2 |
D4 to G2 A2+√3 A2 |
|---|---|---|---|---|
| Dynkin | ||||
| Coxeter | ||||
| Cartan | ||||
| Roots | 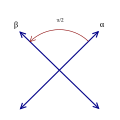 4 roots |
 6 roots |
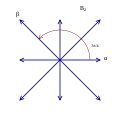 12 roots 4×2 roots |
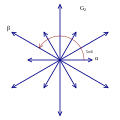 24 roots 6×2 roots |
| Polytope | 
|

|

|

|
Here I2(p) as a folding of Ap-1. I2(p) is considered the undirected group, while this article references the directed ones.
| Crystallographic | Non-crystallographic | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Simply-laced group folding |
A2 → I2(3)×2 → I2(6) |
A3 → I2(3)×2 → G2 |
A4 → I2(5)×2 → I2(10) |
A5 → I2(5)×2 → I2(10) |
A6 → I2(7)×2 → I2(14) |
A7 → I2(7)×2 → I2(14) |
A8 → I2(9)×2 → I2(18) | ||
| Dynkin | |||||||||
| Coxeter | |||||||||
| Plane | A2 | A4 | A6 | A8 | |||||
| Roots Polytope |
 6 roots 6×1 roots |
 12 roots 6×2 roots |
 20 roots 10×2 roots |
 30 roots 10×3 roots |
 42 roots 14×3 roots |
 56 roots 14×4 roots |
 72 roots 18×4 roots | ||
| Ring Radius ratios |
1 | √3:1 | φ:1 | φ:1:? | ?:?:1 | ?:?:?:1 | ?:?:?:1 | ||
References
[edit]- Quaternionic Roots of E 8 Related Coxeter Graphs and Quasicrystals Mehmet KOCA, Nazife Ozdes KOCA, 1998 [1]
- Noncrystallographic Coxeter group H4 in E8 Mehmet Koca, Ramazan Koc and Muataz Al-Barwani, 2001
- Icosidodecahedron from D6 John Baez / 1 January, 2015

![{\displaystyle \left[{\begin{smallmatrix}2&0\\0&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58d402f7fd38428fe2ac791f5a5d12bf7832c69f)
![{\displaystyle \left[{\begin{smallmatrix}2&-1\\-1&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18cb26b504d63dba11f3a12c7ee8fa25fe3bdf0a)
![{\displaystyle \left[{\begin{smallmatrix}2&-2\\-1&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07ca67f2863fd2e6f5a6d91133f30d43a1c95805)
![{\displaystyle \left[{\begin{smallmatrix}2&-3\\-1&2\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c7be0787569951e9dec7fcaaa46c6481f37d3a6)