Regular tetrahedron

Regular tetrahedron
Type	Deltahedron Platonic solid Pyramid
Faces	4 equilateral triangles
Edges	6
Vertices	4
Symmetry group	tetrahedral symmetry $\mathrm {T} _{\mathrm {h} }$
Dual polyhedron	self-dual
Properties	convex
Net

A regular tetrahedron is a polyhedron with four equilateral triangular faces.

Description

Classifications

A regular tetrahedron is a tetrahedron (that is, a four-sided polyhedron) in which all four faces are equilateral triangles. In other words, all of its faces are the same size and shape (congruent), and all edges are the same length. As a convex polyhedron, the regular tetrahedron is the simplest deltahedron, a polyhedron all of whose faces are equilateral triangles; there are seven other convex deltahedra. Like the other pyramids and all tetrahedra in general, the regular tetrahedron is self-dual, meaning its dual is a regular tetrahedron itself.

Regular tetrahedron, representing the classical element of fire, sketched by Johannes Kepler.

Kepler's Platonic solid model of the Solar System

The regular tetrahedron is also one of the five regular Platonic solids—polyhedra in which all of their faces are regular polygons. Known since antiquity, Platonic solids are named after the Greek philosopher Plato, who associated four of those solids with fundamental natural elements. He assigned the regular tetrahedron to the classical element of fire, because its corner is sharpest and most penetrating. Following its attribution with nature by Plato, Johannes Kepler in his Harmonices Mundi sketched each of the Platonic solids. In his Mysterium Cosmographicum, Kepler also proposed the Solar System by using the Platonic solids, setting one inside another and separating them with six spheres resembling the six planets. The ordered solids started from the innermost to the outermost: regular octahedron, regular icosahedron, regular dodecahedron, regular tetrahedron, and cube.

Regular tetrahedron is the degenerated antiprism.

Cartesian coordinates

One way to construct a regular tetrahedron is by using the following Cartesian coordinates, defining the four vertices of a tetrahedron with edge length 2, centered at the origin, and two-level edges:$$\left(\pm 1,0,-{\frac {1}{\sqrt {2}}}\right)\qquad \left(0,\pm 1,{\frac {1}{\sqrt {2}}}\right)$$

A regular tetrahedron can be embedded inside a cube in two ways such that each vertex is a vertex of the cube, and each edge is a diagonal of one of the cube's faces. For one such embedding, the Cartesian coordinates of the vertices are$${\begin{aligned}(1,1,1),&\quad (1,-1,-1),\\(-1,1,-1),&\quad (-1,-1,1).\end{aligned}}$$This yields a tetrahedron with edge-length $2{\sqrt {2}}$, centered at the origin. For the other tetrahedron (which is dual to the first), reverse all the signs. These two tetrahedra's vertices combined are the vertices of a cube, demonstrating that the regular tetrahedron is the 3-demicube, a polyhedron that is by alternating a cube. This form has Coxeter diagram and Schläfli symbol $\mathrm {h} \{4,3\}$.

Properties

Measurement

3D model of a regular tetrahedron

Consider a regular tetrahedron with edge length $a$. Its height is$$h={{\sqrt {\frac {2}{3}}}a}.$$Its surface area is four times the area of an equilateral triangle:$$A=4\cdot \left({\frac {\sqrt {3}}{4}}a^{2}\right)=a^{2}{\sqrt {3}}\approx 1.732a^{2}.$$The volume is one-third of the base times the height, the general formula for a pyramid; this can also be found by dissecting a cube into a tetrahedron and four triangular pyramids.$$V={\frac {1}{3}}\cdot \left({\frac {\sqrt {3}}{4}}a^{2}\right)\cdot {\frac {\sqrt {6}}{3}}a={\frac {a^{3}}{6{\sqrt {2}}}}\approx 0.118a^{3}.$$Its dihedral angle—the angle formed by two planes in which adjacent faces lie—is ${\textstyle \arccos \left(1/3\right)=\arctan \left(2{\sqrt {2}}\right)\approx 70.529^{\circ }.}$

The radii of its circumsphere $R$, insphere $r$, midsphere $r_{\mathrm {M} }$, and exsphere $r_{\mathrm {E} }$ are: $${\begin{aligned}R={\sqrt {\frac {3}{8}}}a,&\qquad r={\frac {1}{3}}R={\frac {a}{\sqrt {24}}},\\r_{\mathrm {M} }={\sqrt {rR}}={\frac {a}{\sqrt {8}}},&\qquad r_{\mathrm {E} }={\frac {a}{\sqrt {6}}}.\end{aligned}}$$For a regular tetrahedron with side length $a$ and circumsphere radius $R$, the distances $d_{i}$ from an arbitrary point in 3-space to its four vertices satisfy the equations: $${\begin{aligned}{\frac {d_{1}^{4}+d_{2}^{4}+d_{3}^{4}+d_{4}^{4}}{4}}+{\frac {16R^{4}}{9}}&=\left({\frac {d_{1}^{2}+d_{2}^{2}+d_{3}^{2}+d_{4}^{2}}{4}}+{\frac {2R^{2}}{3}}\right)^{2},\\4\left(a^{4}+d_{1}^{4}+d_{2}^{4}+d_{3}^{4}+d_{4}^{4}\right)&=\left(a^{2}+d_{1}^{2}+d_{2}^{2}+d_{3}^{2}+d_{4}^{2}\right)^{2}.\end{aligned}}$$

With respect to the base plane the slope of a face (2√2) is twice that of an edge (√2), corresponding to the fact that the horizontal distance covered from the base to the apex along an edge is twice that along the median of a face. In other words, if C is the centroid of the base, the distance from C to a vertex of the base is twice that from C to the midpoint of an edge of the base. This follows from the fact that the medians of a triangle intersect at its centroid, and this point divides each of them in two segments, one of which is twice as long as the other (see proof).

Its solid angle at a vertex subtended by a face is ${\textstyle \arccos \left({\frac {23}{27}}\right)={\frac {\pi }{2}}-3\arcsin \left({\frac {1}{3}}\right)=3\arccos \left({\frac {1}{3}}\right)-\pi ,}$ or approximately 0.55129 steradians, 1809.8 square degrees, and 0.04387 spats.

Symmetry

Main article: Tetrahedral symmetry

The cube and tetrahedron

The proper rotations, (order-3 rotation on a vertex and face, and order-2 on two edges) and reflection plane (through two faces and one edge) in the symmetry group of the regular tetrahedron

The vertices of a cube can be grouped into two groups of four, each forming a regular tetrahedron, showing one of the two tetrahedra in the cube. The symmetries of a regular tetrahedron correspond to half of those of a cube: those that map the tetrahedra to themselves, and not to each other. The tetrahedron is the only Platonic solid not mapped to itself by point inversion.

The regular tetrahedron has 24 isometries, forming the symmetry group known as full tetrahedral symmetry $\mathrm {T} _{\mathrm {d} }$, which is isomorphic to the symmetric group $S_{4}$. This point group has rotational tetrahedral symmetry $\mathrm {T}$, which is isomorphic to alternating group $A_{4}$ (the identity and 11 proper rotations); six reflections in a plane perpendicular to an edge, six reflections in a plane combined with 90° rotation about an axis perpendicular to the plane, consisted of three axes, two per axis, together six (equivalently, they are 90° rotations combined with inversion).

Orthogonal projections of the regular tetrahedron

The regular tetrahedron has two special orthogonal projections, one centered on a vertex or equivalently on a face, and one centered on an edge. The first corresponds to the A₂ Coxeter plane.

Orthographic projection

Centered by	Face/vertex	Edge
Image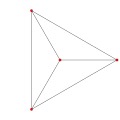
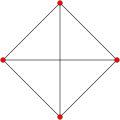
Projective symmetry	[3]	[4]

Related figures

Stellations

Compounds of tetrahedra

Left to right: compound of two tetrahedra, compound of five tetrahedra, compound of ten tetrahedra

The stellated octahedron is constructed by extending its faces to form equilateral triangles on each regular octahedron's face. In the perspective of polyhedral compounds, this figure comprises two such dual tetrahedra, a self-dual because of sharing a common intersphere in the center. Another interesting polyhedral compound involves five intersecting tetrahedra, which has been known for hundreds of years. It comes up regularly in the world of origami. Joining the twenty vertices would form a regular dodecahedron. There are both left-handed and right-handed forms, which are mirror images of each other. Superimposing both forms gives a compound of ten tetrahedra, in which the ten tetrahedra are arranged as five pairs of stellae octangulae.

Construction of polyhedra

Truncated tetrahedron and its dual, the triakis tetrahedron

Many polyhedra are constructed involving regular tetrahedra. By truncating the vertices of a regular tetrahedron, it becomes a truncated tetrahedron. The dual of this solid is the triakis tetrahedron, a regular tetrahedron with four triangular pyramids attached to each of its faces. i.e., its Kleetope. Some Johnson solid such as elongated triangular pyramid and elongated triangular bipyramid are constructed by attaching one and two regular tetrahedra onto the bases of a triangular prism; the triangular bipyramid is constructed by attaching two regular tetrahedra face-to-face.

Regular tetrahedra can be stacked face-to-face in a chiral aperiodic chain called the Boerdijk–Coxeter helix.

Four-dimensional figures

The pentachoron is a four-dimensional polytope, a generalization of a tetrahedron in four-dimensional space. It is bounded by five regular tetrahedra, known as cells.

In four dimensions, all the convex regular 4-polytopes with tetrahedral cells (the 5-cell, 16-cell and 600-cell) can be constructed as tilings of the 3-sphere by these chains, which become periodic in the three-dimensional space of the 4-polytope's boundary surface.

Honeycombs

Five tetrahedra are laid flat on a plane, with the highest 3-dimensional points marked as 1, 2, 3, 4, and 5. These points are then attached and a thin volume of a space is left, where the five edge angles do not quite meet.

Regular tetrahedra alone do not tessellate (fill space), but if alternated with regular octahedra in the ratio of two tetrahedra to one octahedron, they form the alternated cubic honeycomb, which is a tessellation. Some tetrahedra that are not regular, including the Schläfli orthoscheme and the Hill tetrahedron, can tessellate.

Spherical tetrahedron

Spherical tetrahedron

{The tetrahedron can also be represented as a spherical tiling (of spherical triangles), and projected onto the plane via a stereographic projection. This projection is conformal, preserving angles but not areas or lengths. Straight lines on the sphere are projected as circular arcs on the plane.

Cross section of regular tetrahedron

A central cross section of a regular tetrahedron is a square

The two skew perpendicular opposite edges of a regular tetrahedron define a set of parallel planes. When one of these planes intersects the tetrahedron, the resulting cross-section is a rectangle. When the intersecting plane is near one of the edge,s the rectangle is long and skinny. When halfway between the two edges the intersection is a square. The aspect ratio of the rectangle reverses as you pass this halfway point. For the midpoint square intersection, the resulting boundary line traverses every face of the tetrahedron similarly. If the tetrahedron is bisected on this plane, both halves become wedges.

References

Bibilographies

• Alsina, C.; Nelsen, R. B. (2015). A Mathematical Space Odyssey: Solid Geometry in the 21st Century. Mathematical Association of America. ISBN 978-1-61444-216-5.
• Berman, Martin (1971). "Regular-faced convex polyhedra". Journal of the Franklin Institute. 291 (5): 329–352. doi:10.1016/0016-0032(71)90071-8. MR 0290245.
• Brigaglia, Aldo; Palladino, Nicla; Vaccaro, Maria Alessandra (2018). "Historical notes on star geometry in mathematics, art and nature". In Emmer, Michele; Abate, Marco (eds.). Imagine Math 6: Between Culture and Mathematics. Springer International Publishing. pp. 197–211. doi:10.1007/978-3-319-93949-0_17. hdl:10447/325250. ISBN 978-3-319-93948-3.
• Coxeter, H. S. M. (1948). Regular Polytopes. Methuen and Co.
• Cromwell, Peter R. (1997). Polyhedra. Cambridge University Press. ISBN 978-0-521-55432-9.
• Cundy, H. Martyn (1952). "Deltahedra". The Mathematical Gazette. 36 (318): 263–266. doi:10.2307/3608204. JSTOR 3608204. S2CID 250435684.
• Kuchel, Philip W. (2012). "96.45 Can you 'bend' a truncated truncated tetrahedron?". The Mathematical Gazette. 96 (536): 317–323. doi:10.1017/S0025557200004666. JSTOR 23248575.
• Livio, Mario (2003) [2002]. The Golden Ratio: The Story of Phi, the World's Most Astonishing Number (First trade paperback ed.). New York City: Broadway Books. ISBN 0-7679-0816-3.
• Miyazaki, K.; Ishii, M. (2021). "Symmetry in Projection of 4-Dimensional Regular Polychora". In Darvas, György (ed.). Complex Symmetries. doi:10.1007/978-3-030-88059-0. ISBN 978-3-030-88059-0.
• Park, Poo-Sung (2016). "Regular polytope distances" (PDF). Forum Geometricorum. 16: 227–232. Archived from the original (PDF) on 10 October 2016. Retrieved 24 May 2016.
• Posamentier, Alfred S.; Maresch, Guenter; Thaller, Bernd; Spreitzer, Christian; Geretschlager, Robert; Stuhlpfarrer, David; Dorner, Christian (2022). Geometry In Our Three-dimensional World. World Scientific. pp. 267–268. ISBN 9789811237126.
• Pugh, Anthony (1976). Polyhedra: A Visual Approach. University of California Press. ISBN 9780520030565.
• Shavinina, Larisa V. (2013). The Routledge International Handbook of Innovation Education. Routledge. ISBN 978-0-203-38714-6.
• Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 978-0-486-23729-9.